Как сравнить смешанные числа. Сравнение дробей: правила, примеры, решения
Сравнение смешанных чисел: правила, примеры, решения.
В этой статье речь пойдет про сравнение смешанных чисел. Сначала мы разберемся, какие смешанные числа называются равными, а какие – неравными. Дальше мы приведем правило сравнения неравных смешанных чисел, которое позволяет выяснить, какое число больше, а какое – меньше, и рассмотрим примеры. Наконец, мы остановимся на сравнении смешанных чисел с натуральными числами и обыкновенными дробями.
Навигация по странице.
Равные и неравные смешанные числа
Сначала нужно знать, какие смешанные числа называются равными, а какие – неравными. Дадим соответствующие определения.
Равные смешанные числа – это смешанные числа, у которых равны и целые части, и дробные части.
Иными словами, два смешанных числа называются равными, если их записи полностью совпадают. Если же записи смешанных чисел отличаются, то такие смешанные числа называют неравными.
Неравные смешанные числа – это смешанные числа, записи которых отличаются.
Озвученные определения позволяют с одного взгляда определить, равны ли данные смешанные числа или нет. Например, смешанные числа 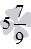 и
и 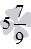 равные, так как их записи полностью совпадают. Эти числа имеют равные целые части и равные дробные части. А смешанные числа
равные, так как их записи полностью совпадают. Эти числа имеют равные целые части и равные дробные части. А смешанные числа  и
и 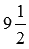 – неравные, так как они имеют неравные целые части. Другими примерами неравных смешанных чисел являются
– неравные, так как они имеют неравные целые части. Другими примерами неравных смешанных чисел являются 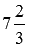 и
и  , а также
, а также  и
и  .
.
Иногда возникает необходимость выяснить, какое из двух неравных смешанных чисел больше другого, а какое – меньше. Как это делается, рассмотрим в следующем пункте.
Сравнение смешанных чисел
Для примера, сравним смешанное число  и смешанное число
и смешанное число 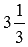 , представив их в виде неправильных дробей. Имеем
, представив их в виде неправильных дробей. Имеем  и
и  . Так сравнение исходных смешанных чисел сводится к сравнению дробей с разными знаменателями
. Так сравнение исходных смешанных чисел сводится к сравнению дробей с разными знаменателями  и
и  . Так как
. Так как 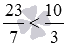 , то
, то 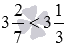 .
.
Сравнение смешанных чисел через сравнение равных им дробей является не лучшим решением. Гораздо удобнее использовать следующее правило сравнения смешанных чисел: больше то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, дробная часть которого больше.
Рассмотрим, как происходит сравнение смешанных чисел по озвученному правилу. Для этого разберем решения примеров.
Сравните смешанные числа  и
и  .
.
Целая часть смешанного числа  меньше целой части смешанного числа
меньше целой части смешанного числа  ( 5<31 смотрите сравнение натуральных чисел), поэтому
( 5<31 смотрите сравнение натуральных чисел), поэтому  .
.
 .
.
Какое из смешанных чисел  и
и  больше?
больше?
Целые части сравниваемых смешанных чисел равны, поэтому сравнение сводится к сравнению дробных частей  и
и  . Так как
. Так как  , то
, то  . Таким образом, смешанное число
. Таким образом, смешанное число  больше, чем смешанное число
больше, чем смешанное число  .
.
 .
.
Сравнение смешанного числа и натурального числа
Разберемся, как сравнить смешанное число и натуральное число.
Справедливо такое правило сравнения смешанного числа с натуральным числом: если целая часть смешанного числа меньше данного натурального числа, то смешанное число меньше данного натурального числа, а если целая часть смешанного числа больше или равна данному смешанному числу, то смешанное число больше данного натурального числа.
Разберем примеры сравнения смешанного числа и натурального числа.
Сравните числа 6 и  .
.
Целая часть смешанного числа  равна 9 . Так как она больше натурального числа 6 , то
равна 9 . Так как она больше натурального числа 6 , то  .
.
 .
.
Дано смешанное число 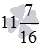 и натуральное число 34 , какое из чисел меньше?
и натуральное число 34 , какое из чисел меньше?
Целая часть смешанного числа 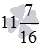 меньше числа 34 ( 11<34 ), поэтому
меньше числа 34 ( 11<34 ), поэтому  .
.
смешанное число 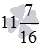 меньше, чем число 34 .
меньше, чем число 34 .
Выполните сравнение числа 5 и смешанного числа  .
.
Целая часть данного смешанного числа равна натуральному числу 5 , следовательно, данное смешанное число больше, чем 5 .
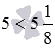 .
.
В заключение этого пункта отметим, что любое смешанное число больше единицы. Это утверждение следует из правила сравнения смешанного числа и натурального числа, а также из того, что целая часть любого смешанного числа либо больше 1 , либо равна 1 .
Сравнение смешанного числа и обыкновенной дроби
Сначала скажем про сравнение смешанного числа и правильной дроби. Любая правильная дробь меньше единицы (смотрите правильные и неправильные дроби), следовательно, любая правильная дробь меньше любого смешанного числа (так как любое смешанное число больше 1 ).
Приведем пример: смешанное число  больше любой правильной дроби, в частности, смешанное число
больше любой правильной дроби, в частности, смешанное число  больше дроби
больше дроби  .
.
Сравнение смешанного числа и неправильной дроби можно свести либо к сравнению двух дробей, либо к сравнению двух смешанных чисел. Для этого в первом случае смешанное число нужно представить в виде неправильной дроби, во втором случае – неправильную дробь представить в виде смешанного числа. Второй способ предпочтительнее.
Сравните смешанное число  и дробь 28/3 .
и дробь 28/3 .
Покажем два способа решения.
Первый способ. Переведем смешанное число  в неправильную дробь:
в неправильную дробь:  . Остается сравнить дроби 74/9 и 28/3 , имеем
. Остается сравнить дроби 74/9 и 28/3 , имеем  . Следовательно,
. Следовательно,  .
.
Второй способ. Выделим целую часть из неправильной дроби 28/3 , имеем  . Теперь сравним смешанные числа
. Теперь сравним смешанные числа  и
и  , получаем
, получаем 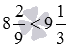 . Следовательно,
. Следовательно,  .
.
 .
.
Сравнение дробей: правила, примеры, решения
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравнение дробей с одинаковыми знаменателями
Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .
Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Произвести сравнение заданных дробей 65 126 и 87 126 .
Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .
Ответ: 87 126 > 65 126 .
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
- найти общий знаменатель;
- сравнить дроби.
Рассмотрим данные действия на примере.
Произвести сравнение дробей 5 12 и 9 16 .
В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48 : 12 = 4 , для второй дроби 9 16 – 48 : 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .
После сравнения дробей получаем, что 20 48 27 48 . Значит, 5 12 меньше 9 16 .
Ответ: 5 12 9 16 .
Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями: если a · d > b · c , тогда a b > c d , но если a · d b · c , тогда a b c d . Рассмотрим сравнение с разными знаменателями.
Произвести сравнение дробей 5 18 и 23 86 .
Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .
Ответ: 5 18 > 23 86 .
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Произвести сравнение дробей 54 19 и 54 31 .
Решение
Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.
Ответ: 54 19 > 54 31 .
Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.
Сравнение дроби с натуральным числом
Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.
Необходимо выполнить сравнение 63 8 и 9 .
Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63 72 , тогда получаем 63 8 72 8 . Значит, заданная дробь меньше целого числа 9 , то есть имеем 63 8 9 .
Сравнение смешанных чисел
Для сравнения смешанных чисел, когда дробные части – правильные дроби используют следующее правило:
При сравнении смешанных чисел больше то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, дробная часть которого больше.


Если попадаются примеры, в которых целые части разные и одна или обе дробные части представляют собой неправильные дроби, сравнение смешанных чисел можно свести к сравнению обыкновенных дробей. Для этого нужно представить смешанные числа в виде неправильных дробей.
Сравним два смешанных числа  и
и  :
:
- Переводим смешанные числа в неправильные дроби:


Приводим неправильные дроби к общему знаменателю:


 , значит
, значит 
Смешанные числа равны, если соответственно равны их целые и дробные части.

Правило сравнения смешанного числа с натуральным числом:
Если целая часть смешанного числа больше или равна данному натуральному числу, то смешанное число больше данного натурального числа, а если целая часть смешанного числа меньше данного натурального числа, то смешанное число меньше данного натурального числа.

Если целая часть смешанного числа меньше данного натурального числа, а дробная часть является неправильной дробью, то сравнение можно свести к сравнению обыкновенных дробей.
Сравним смешанное число  с натуральным числом 6:
с натуральным числом 6:
- Переводим числа в неправильные дроби:


Приводим неправильные дроби к общему знаменателю:


 , значит
, значит 
Любое смешанное число больше любой правильной дроби.

Сравнение смешанного числа c неправильной дробью можно свести к сравнению двух неправильных дробей. Для этого смешанное число нужно представить в виде неправильной дроби.
Сравним смешанное число  с неправильной дробью
с неправильной дробью  :
:
- Переводим смешанное число в неправильную дробь:

Приводим неправильные дроби к общему знаменателю:


 , значит
, значит 
Калькулятор сравнения смешанных чисел
Данный калькулятор поможет вам сравнить смешанные числа. Просто введите два числа и нажмите кнопку Сравнить . Данный калькулятор позволяет также сравнивать: натуральное число с дробью, смешанное число с дробью и натуральное число со смешанным.
Источники:
http://www.cleverstudents.ru/numbers/comparison_of_mixed_numbers.html
http://zaochnik.com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/sravnenie-drobej/
http://naobumium.info/arifmetika/smeshannye_chisla4.php



