Как из 1 целой вычесть дробь. Дроби. Вычитание дробей. Резюме: общая схема вычислений
Вычитание дробей
При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
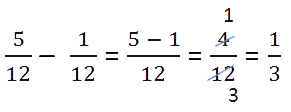
Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так:
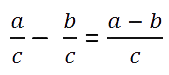
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
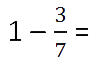 Знаменатель вычитаемой дроби равен 7 , значит, единицу представляют как неправильную дробь
Знаменатель вычитаемой дроби равен 7 , значит, единицу представляют как неправильную дробь
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.
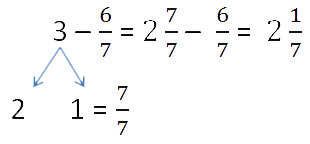 В примере единицу мы заменили неправильной дробью
В примере единицу мы заменили неправильной дробью
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
При подобных расчётах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого (что вычитаем).
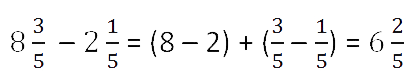
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно привести к общему знаменателю дробные части, а затем выполнить вычитание целой части из целой, а дробной из дробной.
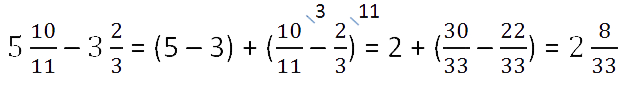
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
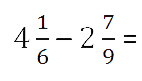
Так как у дробных частей разные знаменатели, то как и во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.
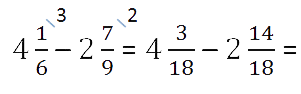
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
Как из целого числа вычесть дробь
Как из целого числа вычесть дробь? Для этого надо целое число представить в виде смешанной дроби.
Мы уже рассмотрели вычитание дроби из единицы. Рассмотрим вычитание дроби из других целых чисел.
Чтобы из целого числа вычесть дробь, надо
1) представить его в виде смешанного числа.
Для этого число уменьшаем на единицу и представить эту единицу в виде дроби, у которой и числитель, и знаменатель равны знаменателю вычитаемого.
2) из смешанного числа вычесть дробь.
Для этого целую часть оставляем без изменения, а из дробной части уменьшаемого вычитаем дробную часть вычитаемого.
С помощью букв правило вычитания дроби из целого числа можно записать так:
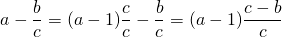
Выполнить вычитание дроби из целого числа:
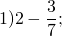
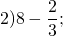
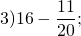
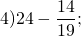
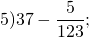
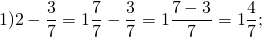
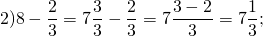
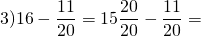
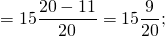
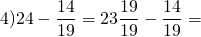
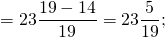
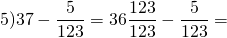
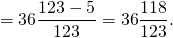
18 Comments
Спасибо, раньше не понимал, сейчас как орешки щелкаю!
Сложение и вычитание дробей
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
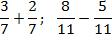
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
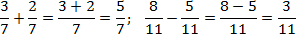
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
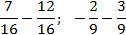
В первом случае все просто, а во втором внесем минусы в числители дробей:
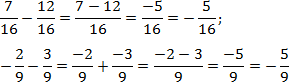
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
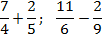
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
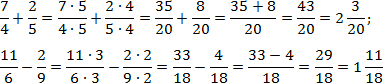
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
- Перевести все дроби, содержащие целую часть, в неправильные. Получим нормальные слагаемые (пусть даже с разными знаменателями), которые считаются по правилам, рассмотренным выше;
- Собственно, вычислить сумму или разность полученных дробей. В результате мы практически найдем ответ;
- Если это все, что требовалось в задаче, выполняем обратное преобразование, т.е. избавляемся от неправильной дроби, выделяя в ней целую часть.
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
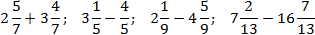
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
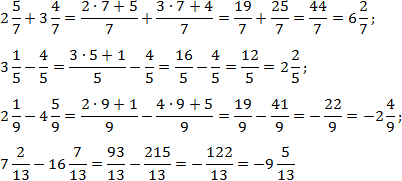
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
- Если в одной или нескольких дробях выделена целая часть, переведите эти дроби в неправильные;
- Приведите все дроби к общему знаменателю любым удобным для вас способом (если, конечно, этого не сделали составители задач);
- Сложите или вычтите полученные числа по правилам сложения и вычитания дробей с одинаковыми знаменателями;
- Если возможно, сократите полученный результат. Если дробь оказалась неправильной, выделите целую часть.
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Источники:
http://math-prosto.ru/?page=pages/drob/subtraction_drobs.php
http://www.for6cl.uznateshe.ru/kak-iz-celogo-chisla-vychest-drob/
http://www.berdov.com/docs/fraction/addition_subtraction/



