Сравнение дробей больше меньше. Как сравнить дроби, не приводя их к общему знаменателю

Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Произвести сравнение заданных дробей 65 126 и 87 126 .

Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .

Ответ: 87 126 > 65 126 .

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

• найти общий знаменатель;
• сравнить дроби.

Рассмотрим данные действия на примере.

Произвести сравнение дробей 5 12 и 9 16 .

В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48 : 12 = 4 , для второй дроби 9 16 – 48 : 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .

После сравнения дробей получаем, что 20 48 27 48 . Значит, 5 12 меньше 9 16 .

Ответ: 5 12 9 16 .

Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями: если a · d > b · c , тогда a b > c d , но если a · d b · c , тогда a b c d . Рассмотрим сравнение с разными знаменателями.

Произвести сравнение дробей 5 18 и 23 86 .

Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.

Ответ: 54 19 > 54 31 .

Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.

Необходимо выполнить сравнение 63 8 и 9 .

Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63 72 , тогда получаем 63 8 72 8 . Значит, заданная дробь меньше целого числа 9 , то есть имеем 63 8 9 .

Сравнение дробей: правила, примеры, решения.

В центре внимания данной статьи стоит сравнение дробей. Мы уже знаем про равные и неравные дроби. Две неравные дроби подлежат дальнейшему сравнению для выяснения, какая дробь больше, а какая дробь меньше. Для сравнения двух дробей существует правило сравнения дробей, которое мы сформулируем ниже, а также разберем примеры применения этого правила при сравнении дробей с одинаковыми и разными знаменателями. В заключение покажем, как сравнить дроби с одинаковыми числителями, не приводя их к общему знаменателю, а также рассмотрим, как сравнить обыкновенную дробь с натуральным числом.

Навигация по странице.

Сравнение дробей с одинаковыми знаменателями

Сравнение дробей с одинаковыми знаменателями по сути является сравнением количества одинаковых долей. К примеру, обыкновенная дробь 3/7 определяет 3 доли 1/7 , а дробь 8/7 соответствует 8 долям 1/7 , поэтому сравнение дробей с одинаковыми знаменателями 3/7 и 8/7 сводится к сравнению чисел 3 и 8 , то есть, к сравнению числителей.

Из этих соображений вытекает правило сравнения дробей с одинаковыми знаменателями: из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та дробь, числитель которой меньше.

Озвученное правило объясняет, как сравнить дроби с одинаковыми знаменателями. Рассмотрим пример применения правила сравнения дробей с одинаковыми знаменателями.

Какая дробь больше: 65/126 или 87/126 ?

Знаменатели сравниваемых обыкновенных дробей равны, а числитель 87 дроби 87/126 больше числителя 65 дроби 65/126 (при необходимости смотрите сравнение натуральных чисел). Поэтому, согласно правилу сравнения дробей с одинаковыми знаменателями, дробь 87/126 больше дроби 65/126 .

.

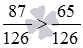Сравнение дробей с разными знаменателями

Сравнение дробей с разными знаменателями можно свести к сравнению дробей с одинаковыми знаменателями. Для этого лишь нужно сравниваемые обыкновенные дроби привести к общему знаменателю.

Итак, чтобы сравнить две дроби с разными знаменателями, нужно

• привести дроби к общему знаменателю;
• сравнить полученные дроби с одинаковыми знаменателями.

Разберем решение примера.

Сравните дробь 5/12 с дробью 9/16 .

Сначала приведем данные дроби с разными знаменателями к общему знаменателю (смотрите правило и примеры приведения дробей к общему знаменателю). В качестве общего знаменателя возьмем наименьший общий знаменатель, равный НОК(12, 16)=48 . Тогда дополнительным множителем дроби 5/12 будет число 48_12=4 , а дополнительным множителем дроби 9/16 будет число 48_16=3 . Получаем 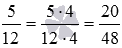и .

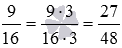Сравнив полученные дроби, имеем 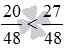. Следовательно, дробь 5/12 меньше, чем дробь 9/16 . На этом сравнение дробей с разными знаменателями завершено.

.

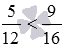Получим еще один способ сравнения дробей с разными знаменателями, который позволит выполнять сравнение дробей без их приведения к общему знаменателю и всех сложностей, связанных с этим процессом.

Для сравнения дробей a/b и c/d , их можно привести к общему знаменателю b·d , равному произведению знаменателей сравниваемых дробей. В этом случае дополнительными множителями дробей a/b и c/d являются числа d и b соответственно, а исходные дроби приводятся к дробям 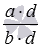и 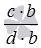с общим знаменателем b·d . Вспомнив правило сравнения дробей с одинаковыми знаменателями, заключаем, что сравнение исходных дробей a/b и c/d свелось к сравнению произведений a·d и c·b .

Отсюда вытекает следующее правило сравнения дробей с разными знаменателями: если a·d>b·c , то 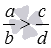, а если a·d 414 , то дробь 5/18 больше, чем дробь 23/86 .

.

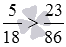Сравнение дробей с одинаковыми числителями

Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.

Существует такое правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.

Рассмотрим решение примера.

Сравните дроби 54/19 и 54/31 .

Так как числители сравниваемых дробей равны, а знаменатель 19 дроби 54/19 меньше знаменателя 31 дроби 54/31 , то 54/19 больше 54/31 .

.

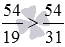В заключение этого пункта приведем пример, хорошо иллюстрирующий основную суть озвученного правила сравнения дробей с одинаковыми числителями. Пусть перед нами две тарелки, на одной из них 1/2 пирога, а на другой 1/16 этого же пирога. Понятно, что скушав половину пирога, мы будем куда больше сыты, чем съев 1/16 его часть.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом сводится к сравнению двух дробей, если число записать в виде дроби со знаменателем 1 (смотрите натуральное число как дробь со знаменателем 1). Рассмотрим решение примера.

Сравните дробь 63/8 и число 9 .

Число 9 можно представить как дробь 9/1 , этим сравнение дроби 63/8 и числа 9 сводится к сравнению дробей 63/8 и 9/1 . После их приведения к общему знаменателю 8 , получаем дроби с одинаковым знаменателем 63/8 и 72/8 . Так как 63<72 , то 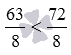, следовательно, .

.

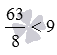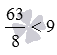fashionat.ru

В этом уроке мы научимся сравнивать дроби между собой. Это очень полезный навык, который необходим для решения целого класса более сложных задач.

Для начала напомню определение равенства дробей:

Дроби a /b и c /d называются равными, если ad = bc .

1. 5/8 = 15/24, поскольку 5 · 24 = 8 · 15 = 120;
2. 3/2 = 27/18, поскольку 3 · 18 = 2 · 27 = 54.

Во всех остальных случаях дроби являются неравными, и для них справедливо одно из следующих утверждений:

1. Дробь a /b больше, чем дробь c /d ;
2. Дробь a /b меньше, чем дробь c /d .

Дробь a /b называется большей, чем дробь c /d , если a /b − c /d > 0.

Дробь x /y называется меньшей, чем дробь s /t , если x /y − s /t

Таким образом, сравнение дробей сводится к их вычитанию. Вопрос: как не запутаться с обозначениями «больше» (>) и «меньше» (

Задача. Сравнить числа:

Следуя определению, вычтем дроби друг из друга:

В каждом сравнении нам потребовалось приводить дроби к общему знаменателю. В частности, используя метод «крест-накрест» и поиск наименьшего общего кратного. Я намеренно не акцентировал внимание на этих моментах, но если что-то непонятно, загляните в урок «Сложение и вычитание дробей » – он совсем легкий.

Сравнение десятичных дробей

В случае с десятичными дробями все намного проще. Здесь не надо ничего вычитать – достаточно просто сравнить разряды. Не лишним будет вспомнить, что такое значащая часть числа. Тем, кто забыл, предлагаю повторить урок «Умножение и деление десятичных дробей » – это также займет буквально пару минут.

Положительная десятичная дробь X больше положительной десятичной дроби Y , если в ней найдется такой десятичный разряд, что:

1. Цифра, стоящая в этом разряде в дроби X , больше соответствующей цифры в дроби Y ;
2. Все разряды старше данного у дробей X и Y совпадают.

1. 12,25 > 12,16. Первые два разряда совпадают (12 = 12), а третий – больше (2 > 1);
2. 0,00697 0,0025, т.к. 0,0025 = 0000,0025 – приписали три нуля слева. Теперь видно, что различие начинается в первом же разряде: 2 > 0.

Конечно, в приведенных примерах с нулями был явный перебор, но смысл именно такой: заполнить недостающие разряды слева, а затем сравнить.

Задача. Сравните дроби:

1. 0,029 ∨ 0,007;
2. 14,045 ∨ 15,5;
3. 0,00003 ∨ 0,0000099;
4. 1700,1 ∨ 0,99501.

По определению имеем:

1. 0,029 > 0,007. Первые два разряда совпадают (00 = 00), дальше начинается различие (2 > 0);
2. 14,045 0,0000099. Здесь надо внимательно считать нули. Первые 5 разрядов в обеих дробях нулевые, но дальше в первой дроби стоит 3, а во второй – 0. Очевидно, 3 > 0;
3. 1700,1 > 0,99501. Перепишем вторую дробь в виде 0000,99501, добавив 3 нуля слева. Теперь все очевидно: 1 > 0 – различие обнаружено в первом же разряде.

К сожалению, приведенная схема сравнения десятичных дробей не универсальна. Этим методом можно сравнивать только положительные числа . В общем же случае алгоритм работы следующий:

1. Положительная дробь всегда больше отрицательной;
2. Две положительные дроби сравниваются по приведенному выше алгоритму;
3. Две отрицательные дроби сравниваются так же, но в конце знак неравенства меняется на противоположный.

Ну как, неслабо? Сейчас рассмотрим конкретные примеры – и все станет понятно.

Задача. Сравните дроби:

1. 0,0027 ∨ 0,0072;
2. −0,192 ∨ −0,39;
3. 0,15 ∨ −11,3;
4. 19,032 ∨ 0,0919295;
5. −750 ∨ −1,45.

1. 0,0027 −0,39. Дроби отрицательные, 2 разряд разный. 1 −11,3. Положительное число всегда больше отрицательного;
2. 19,032 > 0,091. Достаточно вторую дробь переписать в виде 00,091, чтобы увидеть, что различие возникает уже в 1 разряде;
3. −750 001,45. Различие – в первом же разряде.

Как сравнить дроби, не приводя их к общему знаменателю?

При сравнении дробей сначала надо определить, являются ли дроби правильными или неправильными, у неправильной дроби числитель больше знаменателя, у правильной знаменатель больше числителя. Неправильная дробь больше правильной. Если обе дроби правильные, то надо сравнить количество знаков в знаменателях. Дробь у которой количество знаков в знаменателе меньше будет больше. При одинаковых количествах знаков в числителях и в знаменателях надо начать деление числителей на знаменатели до выявления первой большей цифры.

Например, у нас есть 5/10 и 2/3 – как сравнить эти два числа, не приводя дроби к общему знаменателю? Достаточно взять в руки калькулятор (либо смартфон) и выполнить действие, то есть поделить дроби. В итоге получаться числа 0,5 и 0,67, а значит дробь 2/3 больше, чем 5/10.

Во-первых нужно обратить внимание на саму дробь – неправильная будет в любом случае больше правильной. Неправильная – это та, которая имеет больший числитель, нежели знаменатель.

Ну и следующий вариант – это просто напросто произвести процесс деления и увидеть наглядно, какая больше.

Я в таких случаях всегда стараюсь в уме как-то сократить дроби и посмотреть на отношение числителя к знаменателю. Вот пример: есть дробь 7/14 и 3/4. Сократив первую дробь (можно и не сокращать, в принципе) получим 1/2 или половину , ну а 3/4 – явно больше половины (75%). Следовательно, вторая дробь будет больше. Все это считается в уме и quot;автоматическиquot;, естественно.

Ну во первых посмотрите на знаменатель. Если у одной дроби он меньше, наверное это самая меньшая дробь. Потом уже смотрите на числитель. Я например смотрю и прикидываю. Иногда помогает. Может поможет и вам.

Есть парочка дробей, нужно сравнить без приведения к знаменателю общему. Тут можно опробовать несколько фокусов умозрительных.

1. Посмотрите, где правильные, а где неправильные дроби. С первыми просто – числитель поменьше знаменателя, там единицы нет, часть какая-то. 5/8. Вторые – требуют более адекватной формы 1+какой-то хвостик, в них числитель обгоняет знаменатель. 8/5. Неправильная дробь больше любой правильной .
2. Можно фантазию включить и ответить на такой вопросец: Сколько не хватает дроби до единички? 5/6 против 7/8. Конечно, выигрывает последнее число, ведь недостает восьмой части, которая гораздо меньше части шестой.
3. Можно сравнивать с половиной. Для этого, возможно, придется наглядности добавить, например, нарисовать круги да в них разрисовать нужные части. Если оба меньше либо больше, то нужно поискать ещ какую дробь для сравнения обеих дробей.

Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

Если мы до решаем эти дроби, то получим числа (frac<20> <4>= 5) и (frac<20> <10>= 2). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Сравните дроби с одинаковым числителем (frac<1><17>) и (frac<1><15>) .

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

Пример №2:
Сравните правильную дробь с единицей?

Решение:
Любая правильная дробь всегда меньше 1.

Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac<5> <10>).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac<3> <5>).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

(begin&frac<3> <5>= frac<3 times 2> <5 times 2>= frac<6><10>\\&frac<5> <10>b·c , то , а если a·d 414 , то дробь 5/18 больше, чем дробь 23/86 .

Сравнение дробей с одинаковыми числителями

Дроби с одинаковыми числителями и разными знаменателями, несомненно, можно сравнивать с помощью правил, разобранных в предыдущем пункте. Однако, результат сравнения таких дробей легко получить, сравнив знаменатели этих дробей.

Существует такое правило сравнения дробей с одинаковыми числителями : из двух дробей с одинаковыми числителями больше та, у которой меньше знаменатель, и меньше та дробь, знаменатель которой больше.

Рассмотрим решение примера.

Сравните дроби 54/19 и 54/31 .

Так как числители сравниваемых дробей равны, а знаменатель 19 дроби 54/19 меньше знаменателя 31 дроби 54/31 , то 54/19 больше 54/31 .

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше . На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.

Получается, что делили каждый целый круг на одно и то же число 5 , а брали разное количество частей: больше взяли — большая дробь и получилась.

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?

Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?

Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.

Примеры. Сравнить обыкновенные дроби:

Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12: 4=3 ). Для 2-й дроби дополнительный множитель 2 (12: 6=2 ). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9

Источники:

https://zaochnik.com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/sravnenie-drobej/
https://www.cleverstudents.ru/numbers/comparison_of_fractions.html
https://fashionat.ru/kakaya-drob-menshe-kak-sravnit-drobi-ne-privodya-ih-k-obshchemu-znamenatelyu/