Периодическая дробь 5 23 равна. Десятичные дроби, определения, запись, примеры, действия с десятичными дробями. Десятичные дроби на координатном луче

Десятичные дроби: определения, запись, примеры, действия с десятичными дробями

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34 , 21 , 0 , 35035044 , 0 , 0001 , 11 231 552 , 9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой ( 5 . 67 , 6789 . 1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000 , 100 , 10 и др. или смешанное число. Например, вместо 6 10 мы можем указать 0 , 6 , вместо 25 10000 – 0 , 0023 , вместо 512 3 100 – 512 , 03 .

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0 , 14 , которой соответствует 14 100 , читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56 , 002 , которой соответствует 56 2 1000 , мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Что такое разряды в десятичных дробях

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0 , 7 семерка – это десятые доли, в 0 , 0007 – десятитысячные, а в дроби 70 000 , 345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

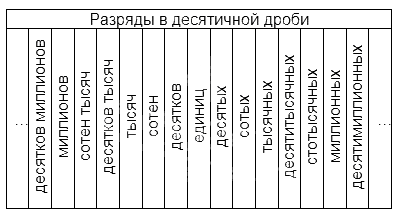
У нас есть десятичная дробь 43 , 098 . У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9 , тысячных – 8 .

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10 -тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Попробуем разложить дробь 56 , 0455 по разрядам.

У нас получится:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56 + 0 , 0455 , или 56 , 0055 + 0 , 4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0 , 367 , 3 , 7 , 55 , 102567958 , 231 032 , 49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5 , 63 мы можем привести к виду 5 63 100 , а 0 , 2 соответствует 2 10 (или любая другая равная ей дробь, например, 4 20 или 1 5 .)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 5 13 нельзя заменить на равную дробь с знаменателем 100 , 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , ( 4 ) , а 76 , 134134134134 … – как 76 , ( 134 ) .

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 ( 7 ) и 0 , 6 ( 77 ) и т.д. Также допустимы записи вида 0 , 67777 ( 7 ) , 0 , 67 ( 7777 ) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0 , 6 ( 7 ) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 ( 34 ) .

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 ( 0 ) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 ( 9 ) , 31 , 6 ( 9 ) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают ( 0 ) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8 , 31 ( 9 ) можно заменить на соответствующую ей дробь 8 , 32 ( 0 ) . Или 4 , ( 9 ) = 5 , ( 0 ) = 5 .

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Положение десятичных дробей на оси координат

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

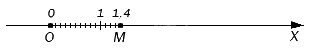
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Дроби. Десятичные дроби.

Десятичная дробь — разновидность дроби, представляющая собой метод представления действительных чисел в виде:

где ± — знак дроби: или +, или -,

, — десятичная запятая, которая служит разделителем меж целой и дробной частями числа,

При этом порядок следования цифр до запятой (слева от неё) имеет конец (как min 1-на цифра), а после запятой (справа) — может быть и конечной (как вариант, цифр после запятой может вообще не быть), и бесконечной.

которое равно сумме конечного либо бесконечного количества слагаемых.

Представление действительных чисел при помощи десятичных дробей есть обобщение записи целых чисел в десятичной системе счисления. В представлении целого числа десятичной дробью нет цифр после запятой, и т.о., это представление выглядит так:

И это совпадает с записью нашего числа в десятичной системе счисления.

Десятичная дробь – это итог деления 1-цы на 10, 100, 1000 и так далее частей. Эти дроби довольно удобны для вычислений, т.к. они основываются на такой же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями практически такие же, как и для целых чисел.

Записывая десятичные дроби не нужно отмечать знаменатель, он определяется местом, занимаемым соответствующей цифрой. Вначале пишем целую часть числа, далее справа ставим десятичную точку. Первая цифра после десятичной точки обозначает число десятых, вторая – число сотых, третья – число тысячных и так далее. Цифры, которые расположены после десятичной точки, являются десятичными знаками.

Например:

Одно из преимуществ десятичных дробей таково, что их очень просто можно привести к виду обыкновенных: число после десятичной точки (у нас это 5047) – это числитель; знаменатель равен n–ой степени 10, где n – число десятичных знаков (у нас это n = 4):

Когда в десятичной дроби нет целой части, значит, перед десятичной точкой ставим нуль:

Свойства десятичных дробей.

1. Десятичная дробь не изменяется, когда справа добавляются нули:

2. Десятичная дробь не изменяется, когда удаляются нули, которые расположены в конце десятичной дроби:

Внимание! Нельзя удалять нули, которые расположенные НЕ в конце десятичной дроби!

3. Десятичная дробь увеличивается в 10, 100, 1000 и так далее раз, когда переносим десятичную точку на соответственно 1-ну, 2, 2 и так далее позиций правее:

3.675 → 367.5 (дробь увеличилась в сто раз).

4. Десятичная дробь становится меньше в десять, сто, тысячу и так далее раз, когда переносим десятичную точку на соответственно 1-ну, 2, 3 и так далее позиций левее:

1536.78 → 1.53678 (дробь стала меньше в тысячу раз).

Виды десятичных дробей.

Десятичные дроби делятся на конечные, бесконечные и периодические десятичные дроби.

Конечная десятичная дробь – это дробь, содержащая конечное количество цифр после запятой (или их там нет совсем), т.е. выглядит так:

Действительное число можно представить как конечную десятичную дробь лишь в том случае, если это число есть рациональным и при записи его несократимой дробью p/q знаменатель q не имеет простых делителей, которые отличны от 2 и 5.

Бесконечная десятичная дробь.

Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, которая называется периодом. Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345).

Периодическая десятичная дробь – это такая бесконечная десятичная дробь, в которой последовательность цифр после запятой, начиная с некоторого места, является периодически повторяющейся группой цифр. Иными словами, периодическая дробь — десятичная дробь, выглядящая так:

Подобную дробь обычно кратко записывают так:

Группа цифр b₁ … b_l, которая повторяется, является периодом дроби, число цифр в этой группе является длиной периода.

Когда в периодической дроби период идет сразу после запятой, значит, дробь является чистой периодической. Когда между запятой и 1-ым периодом есть цифры, то дробь является смешанной периодической, а группа цифр после запятой до 1-го знака периода — предпериодом дроби.

Например, дробь 1,(23) = 1,2323… есть чистой периодической, а дробь 0,1(23)=0,12323… — смешанной периодической.

Основное свойство периодических дробей, благодаря которому их выделяют из всей совокупности десятичных дробей, заключается в том, что периодические дроби и лишь они представляют рациональные числа. Точнее, имеет место следующее:

Любая бесконечная периодическая десятичная дробь представляет рациональное число. Обратно, когда рациональное число раскладывается в бесконечную десятичную дробь, значит, эта дробь будет периодической.

Десятичные дроби, примеры и определения

Дроби записанные в форме 0,8; 0,13; 2,856; 5,2; 0,04 называют десятичными. На самом деле десятичные дроби это упрощенная запись обычных дробей. Эту запись удобно использовать для всех дробей, у которых знаменатели равны 10, 100, 1000 и так далее.

Рассмотрим примеры (0,5 читают как, ноль целых пять десятых);

(0,15 читают как, ноль целых пятнадцать сотых);

(5,3 читают как, пять целых три десятых).

Обратим внимание, что в записи десятичной дроби запятая отделяет целую часть числа от дробной, целая часть правильной дроби рана 0. Запись дробной части десятичной дроби содержит столько цифр, сколько нулей в записи знаменателя соответствующей обыкновенной дроби.

Рассмотрим пример, , , .

В некоторых случаях бывает необходимо рассматривать натуральное число как десятичную дробь, у которой дробная часть равна нулю. Принято записывать что, 5 = 5,0; 245 = 245,0 и так далее. Заметим, что в десятичной записи натурального числа единица младшего разряда в 10 раз меньше единицы соседнего старшего разряда. Таким же свойством обладает запись десятичных дробей. Поэтому сразу после запятой идет разряд десятых, далее разряд сотых, затем разряд тысячных и так далее. Ниже приведены названия разрядов числа 31,85431 первые два столбца — целая часть, остальные столбцы — дробная часть.

Читается эта дробь как тридцать одна целая восемьдесят пять тысяч четыреста тридцать одна стотысячная.

Сложение и вычитание десятичных дробей

Первый способ, это обратить десятичные дроби в обыкновенные и произвести сложение.

как видно из примера этот способ очень неудобный и лучше воспользоваться вторым способом более правильным, не обращая десятичные дроби в обыкновенные. Для того чтобы сложить две десятичные дроби, надо:

• уравнять в слагаемых количество цифр после запятой;
• записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
• сложить полученные числа так, как складывают натуральные числа;
• поставить в полученной сумме запятую под запятыми в слагаемых.

Этим способом так же можно вычитать десятичные дроби. Для того чтобы из одной десятичной дроби вычесть другую, надо:

• уравнять в уменьшаемом и вычитаемом количество цифр после запятой;
• записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
• произвести вычитание так, как вычитают натуральные числа;
• поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.

В рассмотренных выше примерах видно, что сложение и вычитание десятичных дробей выполнялось поразрядно, то есть так, как мы производили аналогичные действия с натуральными числами. Это и есть главное преимущество десятичной формы записи дробей.

Умножение десятичных дробей

Для того чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и так далее цифры. Следовательно, если запятую перенести вправо на 1, 2, 3 и так далее цифры, то дробь увеличится соответственно в 10, 100, 1000 и так далее раз. Для того чтобы перемножить две десятичные дроби, надо:

• умножить их как натуральные числа, не обращая внимания на запятые;
• в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Встречаются случаи, когда произведение содержит меньше цифр, чем требуется отделить запятой, слева перед этим произведением дописывают необходимое количество нулей, а затем переносят запятую влево на нужное количество цифр.

Рассмотрим примеры: 2 * 4 = 8, тогда 0,2 * 0,4 = 0,08; 23 * 35 = 805, тогда 0,023 * 0,35 = 0,00805.

Встречаются случаи, когда один из множителей равен 0,1; 0,01; 0,001 и так далее, удобнее пользоваться следующим правилом.

• Для того чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и так далее, надо в этой десятичной дроби перенести запятую влево соответственно на 1, 2, 3 и так далее цифры.

Рассмотрим примеры: 2,65 * 0,1 = 0,265; 457,6 * 0,01 = 4,576.

Свойства умножения натуральных чисел выполняются и для десятичных дробей.

• ab = ba — переместительное свойство умножения;
• (ab) c = a (bc) — сочетательное свойство умножения;
• a (b + c) = ab + ac — распределительное свойство умножения, относительно сложения.

Деление десятичных дробей

Известно, если разделить натуральное число a на натуральное число b означает найти такое натуральное число c, которое при умножении на b дает число a. Это правило остается верным, если хотя бы одно из чисел a, b, c является десятичной дробью.

Рассмотрим пример, требуется разделить 43,52 на 17 уголком, не обращая внимания на запятую. При этом запятую в частном следует поставить непосредственно перед тем, как будет использована первая цифра после запятой в делимом.

Бывают случаи когда делимое меньше делителя, тогда целая часть частного равна нулю. Рассмотрим пример:

Рассмотрим еще один интересный пример.

Процесс деления остановлен, потому что цифры делимого закончились, а в остатке нуль не получили. Известно, что десятичная дробь не изменится, если к ней справа приписать любое количество нулей. Тогда становится понятно, что цифры делимого закончится не могут.

Для того чтобы разделить десятичную дробь на 10, 100, 1000 и так далее, надо в этой дроби перенести запятую влево на 1, 2, 3 и так далее цифры. Рассмотрим пример: 5,14 : 10 = 0,514; 2 : 100 = 0,02; 37,51 : 1000 = 0,03751.

Если делимое и делитель увеличить одновременно в 10, 100, 1000 и так далее раз, то частное не изменится.

Рассмотрим пример: 39,44 : 1,6 = 24,65 увеличим делимое и делитель в 10 раз 394,4 : 16 = 24,65 справедливо заметить, что делить десятичную дробь на натуральное число во втором примере легче.

Для того чтобы разделить десятичную дробь на десятичную, надо:

• перенести в делимом и в делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
• выполнить деление на натуральное число.

Рассмотрим пример: 23,6 : 0,02 заметим, что в делителе стоит два знака после запятой, следовательно умножаем оба числа на 100 получаем 2360 : 2 = 1180 делим результат на 100 и получаем ответ 11,80 или 23,6 : 0,02 = 11,8.

Сравнение десятичных дробей

Существует два способа сравнения десятичных дробей. Способ первый, требуется сравнить две десятичные дроби 4,321 и 4,32 уравниваем количество знаков после запятой и начинаем сравнивать поразрядно, десятые с десятыми, сотые с сотыми и так далее в итоге получаем 4,321 > 4,320.

Второй способ сравнения десятичных дробей производится с помощью умножения, умножим вышеприведенный пример на 1000 и сравним 4321 > 4320. Какой способ удобней, каждый выбирает для себя сам.

Источники:

http://zaochnik.com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/desjatichnye-drobi-opredelenija-zapis-primery-dejs/
http://www.calc.ru/Drobi-Desyatichnyye-Drobi.html
http://prostoi-sovet.ru/desyatichnye-drobi-primery-i-opredeleniya.html